공부혜옹
백준 2585번 경비행기 본문
경비행기
시간 제한메모리 제한제출정답맞은 사람정답 비율
| 1 초 | 128 MB | 2025 | 683 | 436 | 31.322% |
문제
경비행기 독수리호가 출발지 S에서 목적지 T로 가능한 빠른 속도로 안전하게 이동하고자 한다. 이때, 경비행기의 연료통의 크기를 정하는 것이 중요한 문제가 된다. 큰 연료통을 장착하면 중간에 내려서 급유를 받는 횟수가 적은 장점이 있지만 연료통의 무게로 인하여 속도가 느려지고, 안정성에도 문제가 있을 수 있다. 한편 작은 연료통을 장착하면 비행기의 속도가 빨라지는 장점이 있지만 중간에 내려서 급유를 받아야 하는 횟수가 많아지는 단점이 있다. 문제는 중간에 내려서 급유를 받는 횟수가 k이하 일 때 연료통의 최소용량을 구하는 것이다. 아래 예를 보자.
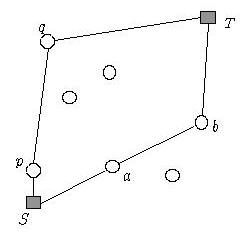
위 그림은 S, T와 7개의 중간 비행장의 위치를 나타내고 있는 그림이다. 위 예제에서 중간급유를 위한 착륙 허용 최대횟수 k=2라면 S-a-b-T로 가는 항로가 S-p-q-T로 가는 항로 보다 연료통이 작게 된다. 왜냐하면, S-p-q-T항로에서 q-T의 길이가 매우 길어서 이 구간을 위해서 상당히 큰 연료통이 필요하기 때문이다. 문제는 이와 같이 중간에 최대 K번 내려서 갈 수 있을 때 최소 연료통의 크기가 얼마인지를 결정하여 출력하면 된다. 참고사항은 다음과 같다.
- 모든 비행기는 두 지점 사이를 반드시 직선으로 날아간다. 거리의 단위는 ㎞이고 연료의 단위는 ℓ(리터)이다. 1ℓ당 비행거리는 10㎞이고 연료주입은 ℓ단위로 한다.
- 두 위치간의 거리는 평면상의 거리이다. 예를 들면, 두 점 g=(2,1)와 h=(37,43)간의 거리 d(g,h)는 (2−37)2+(1−43)2 = 54.671... 이고 50<d(g,h)≤60이므로 필요한 연료는 6ℓ가 된다.
- 출발지 S의 좌표는 항상 (0,0)이고 목적지 T의 좌표는 (10000,10000)으로 모든 입력 데이터에서 고정되어 있다.
- 출발지와 목적지를 제외한 비행장의 수 n은 3≤n≤1000이고 그 좌표 값 (x,y)의 범위는 0<x,y<10000의 정수이다. 그리고 최대 허용 중간급유 횟수 k는 0≤k≤1000이다.
입력
첫 줄에는 n과 k가 하나의 공백을 사이에 두고 주어진다. 그 다음 n개의 줄에는 각 비행장 (급유지)의 정수좌표가 x y 형식으로 주어진다.
출력
S에서 T까지 k번 이하로 중간급유 하여 갈 수 있는 항로에서의 최소 연료통 용량에 해당되는 정수를 출력한다.
#include <iostream>
#include <vector>
#include <utility>
#include <queue>
#include <cstring>
#include <cmath>
using namespace std;
int n;
int k;
int arr[1010][2] = { 0, };
int check[1001];
int BFS(int mid, int start, int canDis) {
memset(check, 0, sizeof(check));
int cnt=0;
double dis = 0.0;
double disTo = 0.0;
int num = 0;
int size = 0;
queue<int> q;
q.push(start);
while (!q.empty()) {
size = q.size();
if (cnt > k) {
return 0;
}
for (int i = 0; i < size; i++) {
num = q.front();
q.pop();
if (!check[num]) {
check[num] = true;
for (int j = 1; j <= n; j++) {
dis = sqrt(pow(arr[num][0] - arr[j][0], 2) + pow(arr[num][1] - arr[j][1], 2));
if (dis <= canDis) {
disTo = sqrt(pow(10000 - arr[j][0], 2) + pow(10000 - arr[j][1], 2));
if (disTo <= canDis) {
return 1;
}
q.push(j);
}
}
}
}
cnt++;
}
return 0;
}
int main() {
cin >> n >> k;
memset(arr, 0, sizeof(arr));
for (int i = 1; i <= n; i++) {
cin >> arr[i][0] >> arr[i][1];
}
int first = 0;
int end = 10000;
int mid=0;
int ans =0;
while (first <= end) {
mid = (first + end) / 2;
int bfs = BFS(mid, 0, mid * 10);
if (bfs) {
ans = mid;
end = mid - 1;
}
else {
first = mid + 1;
}
}
cout << ans;
return 0;
}최소연료통의 용량을 찾기위해 0~10000범위의 용량을 일일히 조건을 충족하는지 BFS로 비교하였다. 당연히 용량 하나하나를 브루트포스식으로 비교하면 초과가 날거같아 이분탐색을 이용했는데 지금 생각해보면 범위의 한계를 10000이 아니라 더 줄였어도 됐을거같다(사실 확신은 없다)
하여튼 이렇게 이분탐색으로 연료통의 용량을 구하고 연료통용량, 시작점, 구한연료통 용량으로 갈 수 있는 최대거리(mid * 10)을 BFS 인자로 넘겨주었다.
BFS에서는 시작점으로 넘겨준 좌표와 1~n까지의 거리를 구한다 그 거리가 구한연료통 용량으로 갈 수 있는 최대거리(disCan)보다 작으면 10000(끝좌표) 부터 1~n까지의 거리를 구해 이것 또한 최대 거리보다 작으면 적합한 연료통용량으로 취급하고 BFS를 종료한다. 두가지 조건중 한가지라도 만족하지 못했을 경우 cnt(현재중간급유횟수)를 증가시키고 BFS를 계속 진행한다.
첫번째조건 두번째조건
|-----------|-------------------------------------|
0 j 10000
'공부합시다 > Algorithm' 카테고리의 다른 글
| 백준 1477번 휴게소 세우기 (0) | 2021.04.07 |
|---|---|
| 백준 11812번 K진 트리 (0) | 2021.04.07 |
| 백준 9202번 Boggle (0) | 2021.04.01 |
| 백준 2872번 우리집엔 도서관이 있어 (0) | 2021.03.30 |
| 백준 2110번 공유기설치 (0) | 2021.03.24 |

